 menu
menu menu
menu



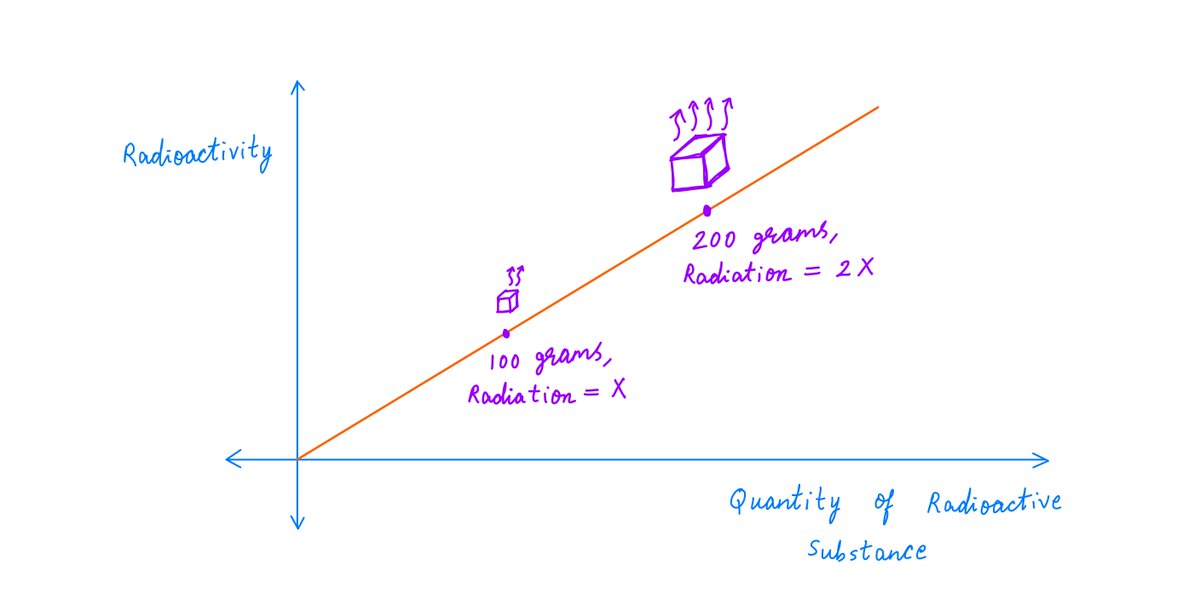
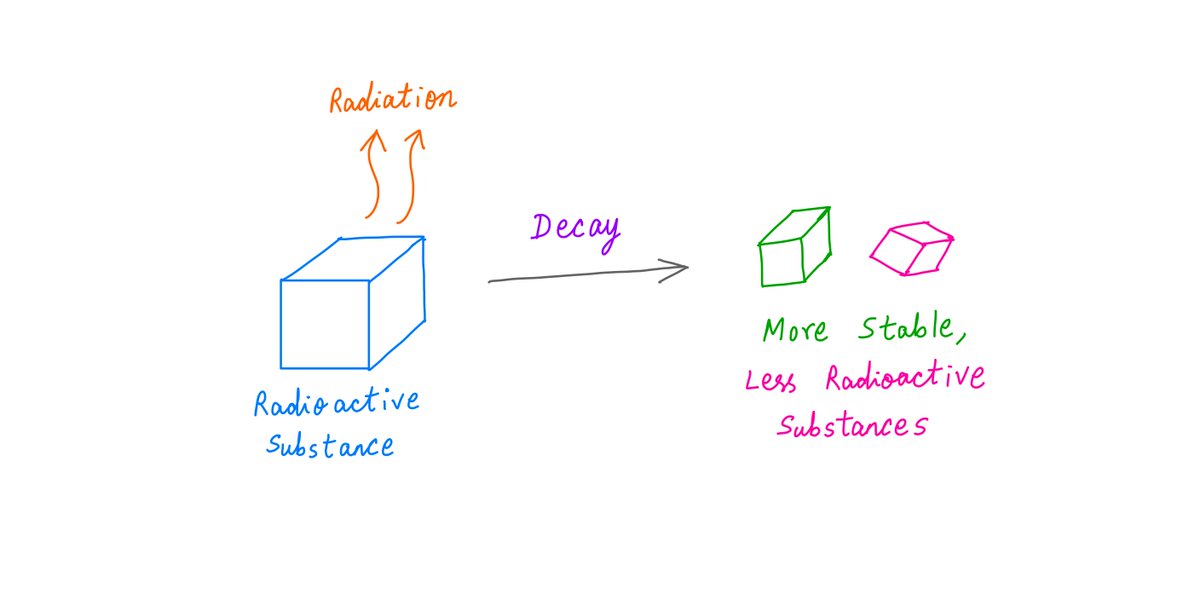
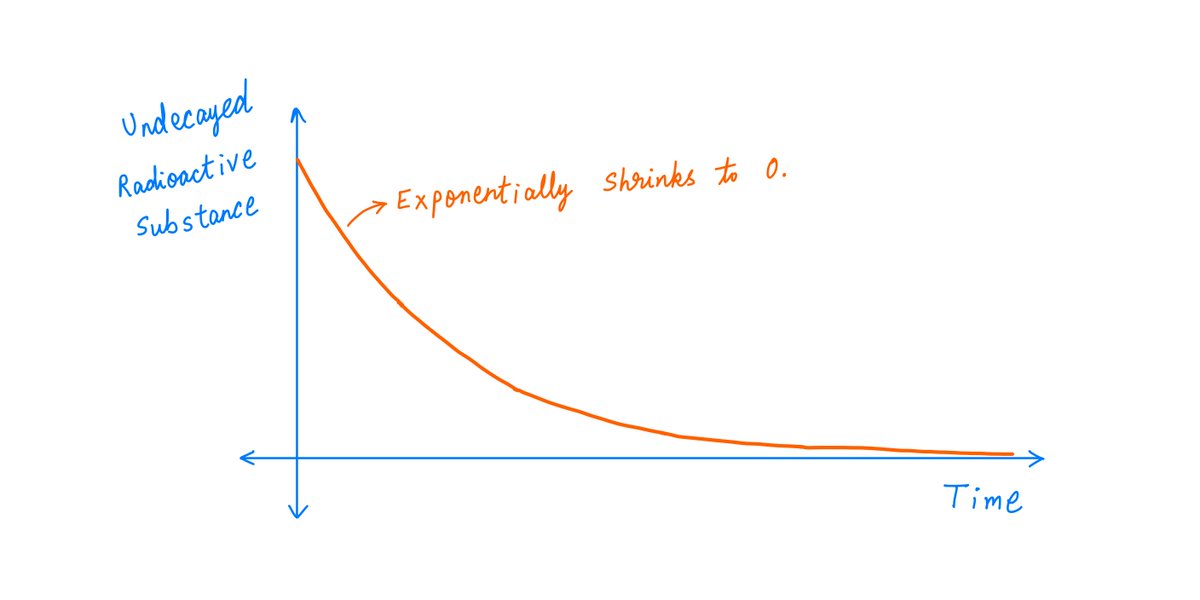
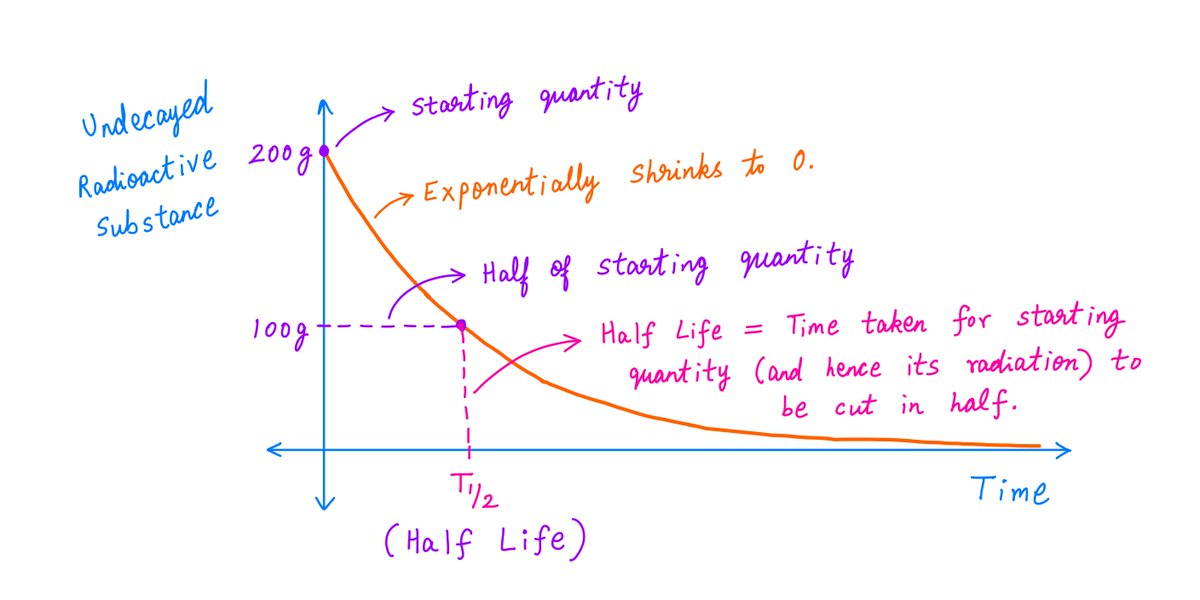



 10-K Diver @10kdiver1/
Get a cup of coffee.
In this thread, I'll walk you through the Rule of 72 -- and related "mental math tricks" for investors. twitter.com
10-K Diver @10kdiver1/
Get a cup of coffee.
In this thread, I'll walk you through the Rule of 72 -- and related "mental math tricks" for investors. twitter.com
 10-K Diver @10kdiver1/
Get a cup of coffee.
In this thread, I'll help you understand the relationships between *investing* and *inflation*. twitter.com
10-K Diver @10kdiver1/
Get a cup of coffee.
In this thread, I'll help you understand the relationships between *investing* and *inflation*. twitter.com Pay what you can
Pay what you can