 menu
menu menu
menu




 10-K Diver @10kdiver1/
Get a cup of coffee.
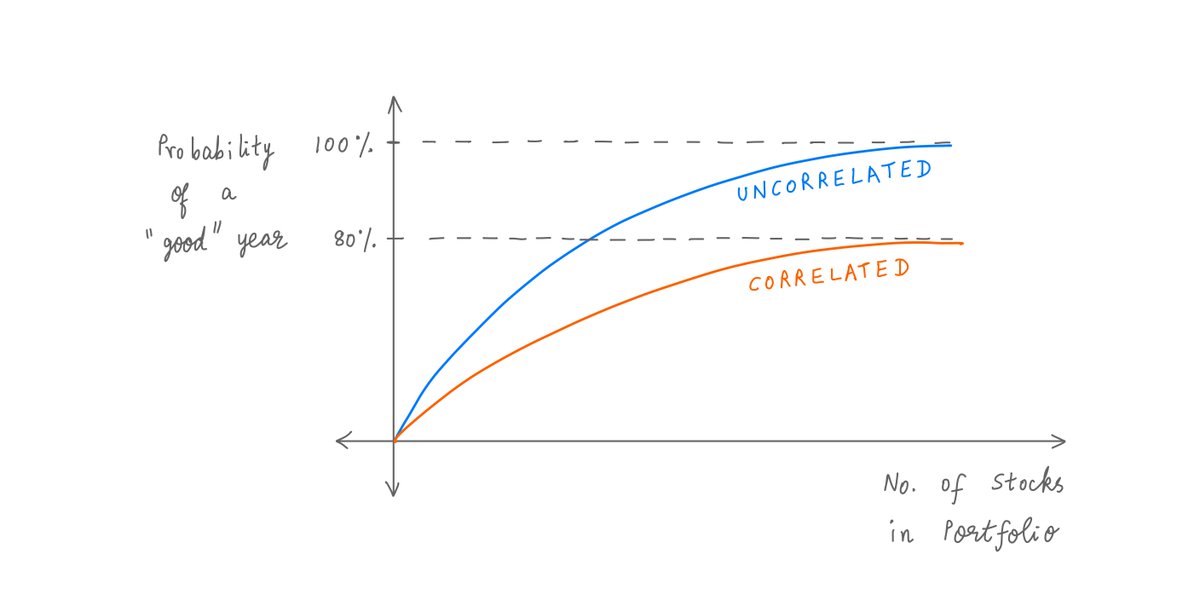
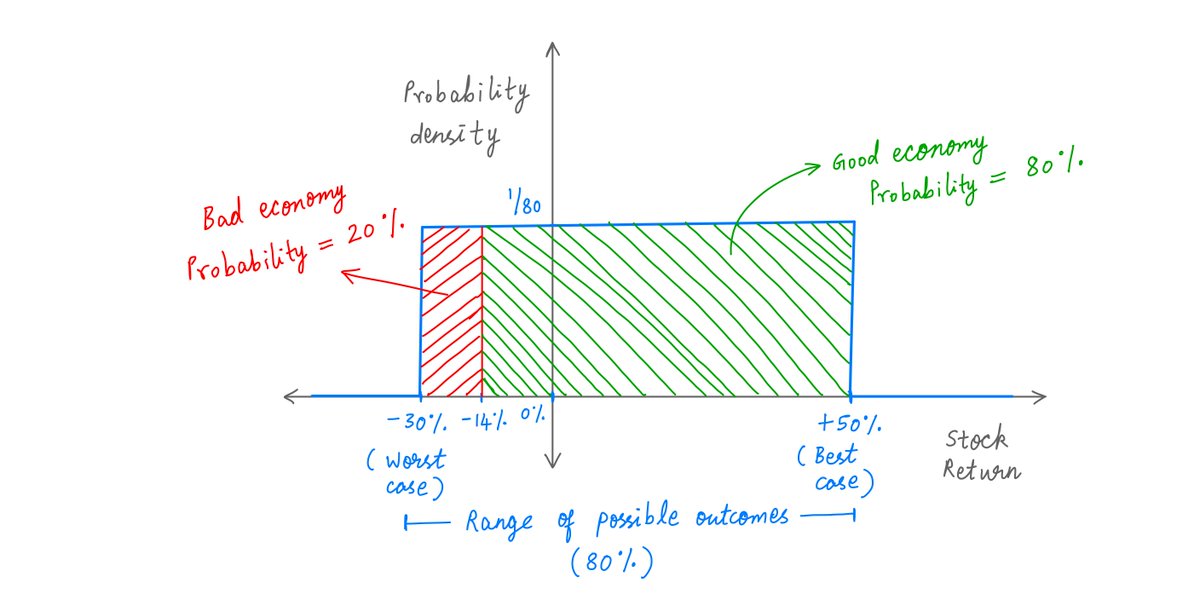
In this thread, I'll walk you through the basics of portfolio diversification. twitter.com
10-K Diver @10kdiver1/
Get a cup of coffee.
In this thread, I'll walk you through the basics of portfolio diversification. twitter.com


 10-K Diver @10kdiver1/
Get a cup of coffee.
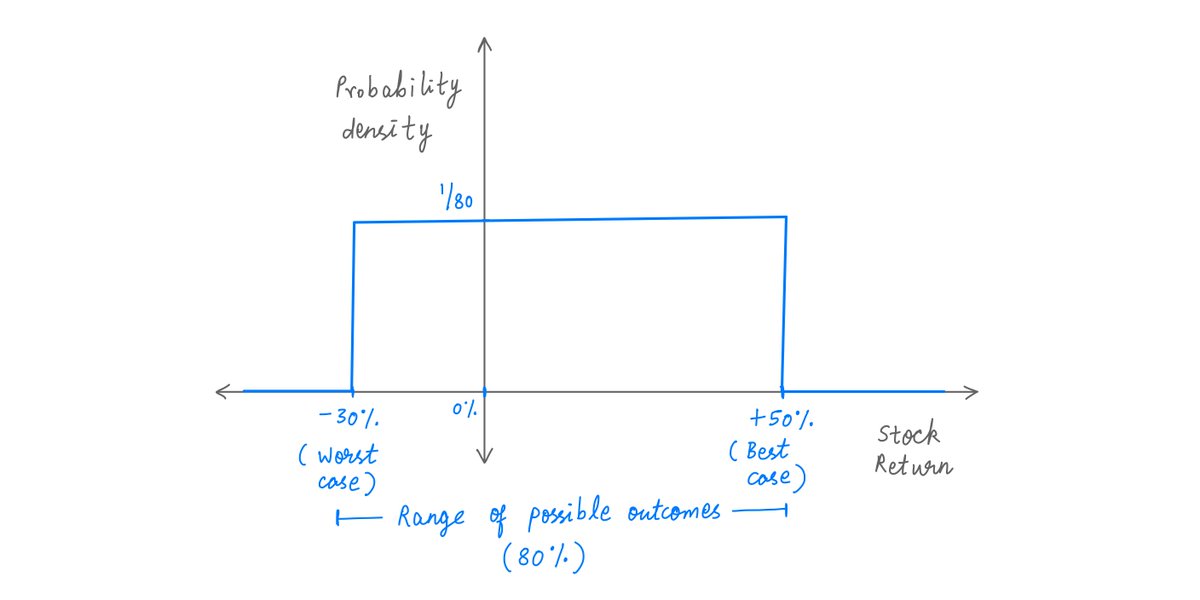
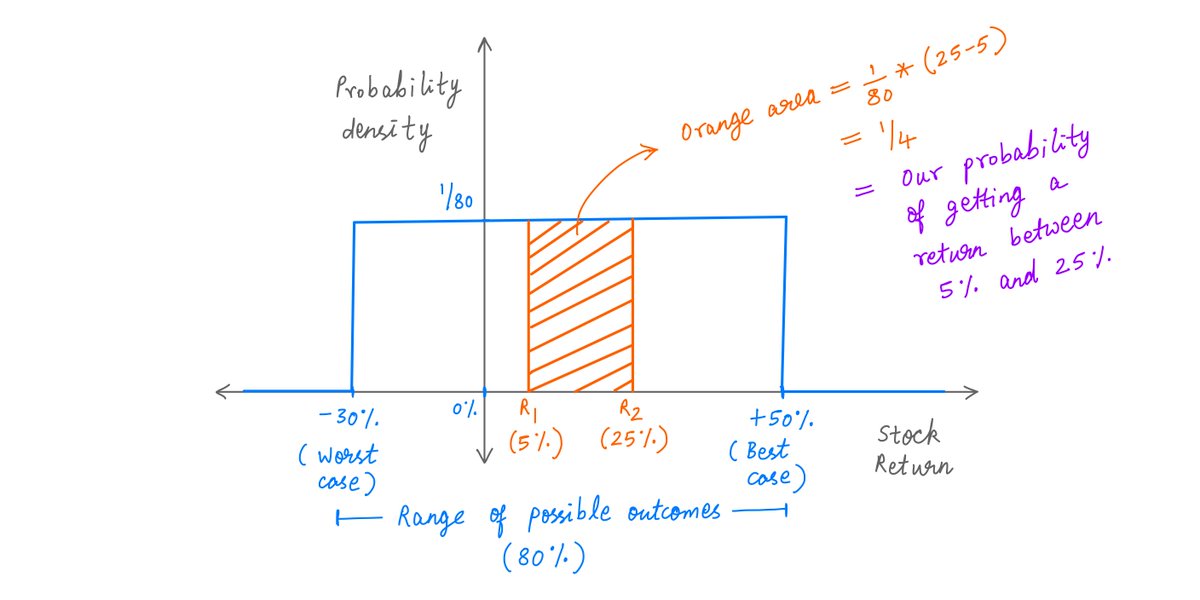
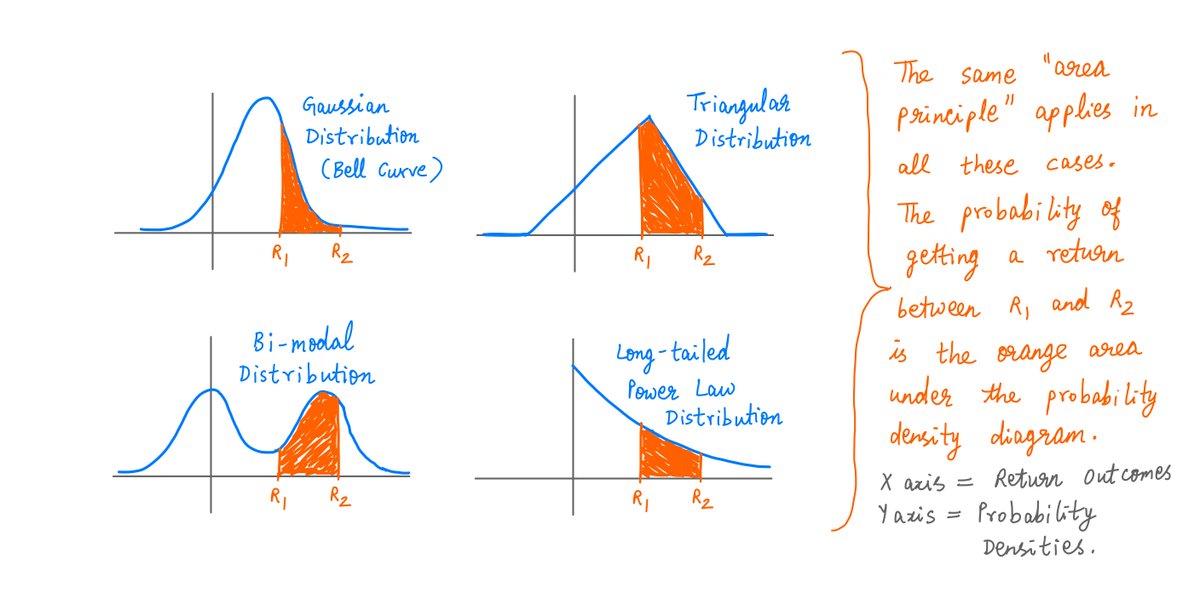
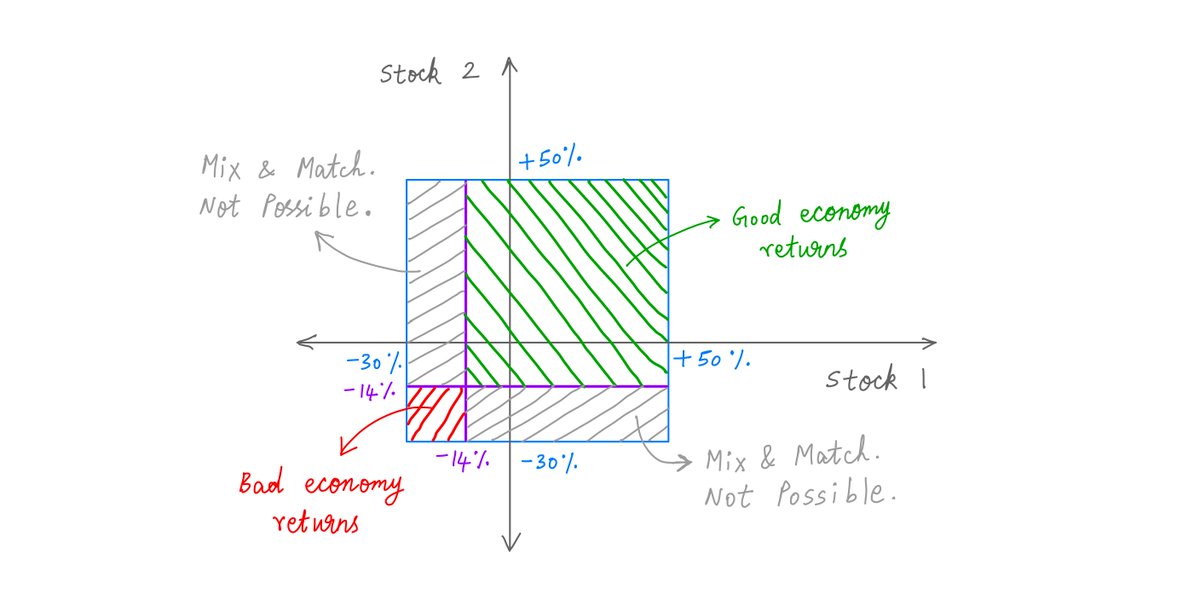
In this thread, I'll walk you through tail risks and their dangers. twitter.com
10-K Diver @10kdiver1/
Get a cup of coffee.
In this thread, I'll walk you through tail risks and their dangers. twitter.com Pay what you can
Pay what you can